Coś takiego, jak „największa liczba”, oczywiście w matematyce nie istnieje, bo do każdej skończonej liczby można jeszcze coś dodać – a nieskończoność też nie jest największa, bo nieskończonych liczb (wbrew intuicji) również istnieje nieskończenie wiele.

W Księdze Rekordów Guinnessa można jednak znaleźć największą (skończoną) liczbę, jaka kiedykolwiek pojawiła się w literaturze naukowej. Jak nietrudno zgadnąć, jest ona (liczba, nie księga) tak wielka, że nie sposób jej normalnie zapisać, a nawet sam opis dojścia do niej zajmie trochę miejsca. Na szczęście jego zrozumienie nie wymaga żadnej poważniejszej wiedzy matematycznej, więc nawet humaniści mogą czytać śmiało.

Jedno nieznane ze szkoły pojęcie trzeba jednak wprowadzić: notacja strzałkowa.

a ↑ b

Powyższy zapis oznacza nic innego jak mnożenie: a * a * a * … * a, w którym liczba czynników jest równa b. W skrócie:

a ↑ b = a^b

Czyli na przykład:

3 ↑ 3 = 3³ = 27

Na razie to nic innego, jak zwykłe potęgowanie – ale sytuacja się zmienia, gdy dodamy drugą strzałkę:

a ↑↑ b

Ten zapis rozwija się następująco:

a ↑ (a ↑ (a ↑ (… ↑ a))) = a^aa...a

…gdzie liczba a znowu pojawia się b razy. Ale tym razem już nie mamy do czynienia z mnożeniem, tylko z potęgowaniem.

Tu właśnie się kryje siła notacji strzałkowej: każda kolejna strzałka oznacza działanie coraz wyższego stopnia. Jak wielka jest to siła? Zobaczmy kolejny przykład:

3 ↑↑ 3 = 3 ↑ (3 ↑ 3) = 3³³ = 3²⁷ = 7 625 597 484 987

Ponad siedem bilionów. Całkiem dużo, jak na tak prosto wyglądające wyrażenie, prawda? A co dopiero, jeśli użyjemy trzech strzałek:

3 ↑↑↑ 3 = 3 ↑↑ (3 ↑↑ 3) = 3 ↑↑ (3 ↑ 3 ↑ 3) = 3^33...3

Ile będzie tych trójek na końcu? Tak, tak – liczba trójek w powyższym łańcuchu potęgowym, to te siedem bilionów z kawałkiem, które otrzymaliśmy w poprzednim kroku! Samo ich zapisanie jest praktyczną niemożliwością – trzeba by do tego około miliona opasłych tomów, ewentualnie ośmiu terabajtowych dysków. A co dopiero obliczenie końcowego wyniku…

Ale OK, spróbujmy chociaż zacząć:

3³³³ = 3^{7 625 597 484 987} ≈ 10^{3 500 000 000 000}

Auć. Już czwarte potęgowanie daje nam liczbę poza wszelkim wyobrażeniem, którą trudno nawet do czegoś porównać. Liczba atomów w obserwowalnym wszechświecie? Skromne 10⁸⁰, śmiech na sali. Objętość tegoż wszechświata, wyrażona w długościach Plancka? Niespełna 4 * 10¹⁸⁶, nadal śmiech na sali. Co by tu zatem… A gdyby każdy atom we wszechświecie zawierał w sobie kolejny wszechświat, a każdy z jego atomów jeszcze kolejny – i tak miliard razy, to ile byłoby w sumie tych wszystkich atomów? Ot, marne 10^{80 000 000 000} – ciągle nawet nie blisko.

Co dostaniemy w kolejnym kroku?

3³³³³ ≈ 3^{103 500 000 000 000} ≈ 10^{101 500 000 000 000}

Poprzednia liczba, już i tak niewyobrażalna, to teraz tylko nieco więcej niż liczba cyfr w kolejnej liczbie. Wszystkich atomów w naszych miliard razy zagnieżdżonych wszechświatach nie wystarczyłoby do zapisania wyniku – i to bardzo grubo by nie wystarczyło, nawet gdyby każdą cyfrę zapisać za pomocą jednego tylko atomu.

A to dopiero pięć trójek. Przed nami jeszcze tylko 7 625 597 484 982…

Tak więc powiedzieć, że liczba 3 ↑↑↑ 3 jest niewyobrażalna, to nic nie powiedzieć. Ta liczba jest niewyobrażalnie niewyobrażalna.

Myślę, że siła notacji strzałkowej nie budzi już w nikim najmniejszych wątpliwości. Nikt też się chyba nie odważy wyliczać wartości zapisu z jeszcze jedną strzałką:

3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3) = 3 ↑↑ (3 ↑↑ (3 ↑↑ … (3 ↑↑ 3)))

Tym razem 3 ↑↑↑ 3 to zaledwie liczba czynników w łańcuchu – ale już nie łańcuchu potęgowym, tylko łańcuchu łańcuchów potęgowych, gdzie liczba trójek w każdym kolejnym to wartość wyliczona z poprzedniego:

3 ↑↑ 3 -> łańcuch trzech trójek, dający 7 625 597 484 987
3 ↑↑ (3 ↑↑ 3) -> łańcuch 7 625 597 484 987 trójek, dający 3 ↑↑↑ 3
3 ↑↑ (3 ↑↑ (3 ↑↑ 3)) -> łańcuch 3 ↑↑↑ 3 trójek, dający… lepiej nie wiedzieć ile
3 ↑↑ (3 ↑↑ (3 ↑↑ (3 ↑↑ 3))) -> łańcuch lepiej nie wiedzieć ilu trójek…

…i tak dalej, 3 ↑↑↑ 3 razy. Oczywiście świat by się zdążył skończyć, i to niewyobrażalnie wiele razy, zanim byśmy wykonali tyle kroków – a wyniku, nawet w postaci potęgowej, nie byłoby gdzie zapisać.

Jeśli zatem poprzednia liczba była niewyobrażalnie niewyobrażalna, to ta jest już niewyobrażalnie^{niewyobrażalnie} niewyobrażalna.

A to jeszcze ciągle nie jest nasza rekordzistka, nie myślcie sobie. Dopiero wchodzimy na właściwą drogę:

G₁ = 3 ↑↑↑↑ 3

No i teraz trzymajcie się mocno:

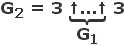
Mam nadzieję, że udało się nie spaść z krzesła.

Trzy strzałki dały nam liczbę poza wszelkim wyobrażeniem. Cztery dałyby liczbę, o której strach w ogóle myśleć. A każda kolejna strzałka, przypominam, oznacza działanie coraz wyższego stopnia (mnożenie, potęgowanie, łańcuch potęgowy, łańcuch łańcuchów…), wykonywane coraz więcej razy, co oznacza coraz szybszy wzrost w porównaniu z poprzednią strzałką – a ten już na samym początku był kosmicznie szybki. Co zatem może wyjść z działania, gdzie liczba, o której strach w ogóle myśleć, jest zaledwie liczbą strzałek?

Każdy chyba przyzna, że na to już dawno zabrakło adekwatnych określeń.

To jednak ciągle nie jest docelowa liczba. Dalej bowiem w analogiczny sposób konstruujemy kolejne: G₃ to liczba z G₂ strzałek, G₄ to liczba z G₃ strzałek – i tak dalej, każda kolejna przewyższająca poprzednią w stopniu nie dającym się nawet nazwać, nie mówiąc o wyobrażeniu…

A liczba, do której od początku zmierzamy, rekordzistka Guinnessa, to, uwaga:

G₆₄

Robi wrażenie, prawda?

Liczba ta zwana jest Liczbą Grahama, od nazwiska matematyka, który ją uzyskał. A uzyskał ją w dowodzie uogólnionego twierdzenia Ramseya, które w swojej podstawowej postaci brzmi tak banalnie, że na pierwszy rzut oka nikt by nawet nie podejrzewał, że mogą z nim się wiązać jakieś duże liczby. Matematyka potrafi jednak potężnie zaskakiwać.

Czasami wręcz niewyobrażalnie.