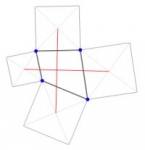
Narysuj czworokąt. Jakikolwiek, może być nawet wklęsły.
Zaznacz środek każdego z boków.
Połącz po kolei te środki.
Uzyskana w ten sposób figura zawsze będzie idealnym równoległobokiem. Zawsze.
Nie wierzysz? Sprawdź, przeciągając wierzchołki myszą:
(Aplet HTML5 może nie działać, jeśli czytasz ten wpis w czytniku RSS lub w badzIEwnej przeglądarce)
Zagadka, jak już się chyba każdy domyślił, brzmi: dlaczego tak się dzieje? Podpowiem, że ma to związek z twierdzeniem pewnego starożytnego Greka;-).








Komentarze
Oj, nie dowodziłem niczego z tej broszki parę ładnych lat, ale dla czworokąta wypukłego dowód [aka wytłumaczenie ;)] na kolanie mam. Numerując wierzchołki po kolei 1..4 otrzymujemy sytuację, gdzie wierzchołki 1,2,3 tworzą kąt z 2 jako wierzchołkiem, a jednocześnie 1-3 tworzą podstawę trójkąta. Owa podstawa jest równoległa do linii łączącej połowy odcinków 1-2 oraz 2-3 na mocy twierdzenia pewnego Greka, ponieważ oba odcinki [podstawa i utworzony] są fragmentami prostych, odkładających z założenia na ramionach kąta 123 odcinki o jednakowych proporcjach [1:1]. Analogicznie dowodzimy dla trójkąta 134, z czego „poprzez” równoległość podstawy do obu odcinków wywodzimy równoległość odcinków 12-23 oraz 34-41. QED. Uzasadnienie dla czworokąta wklęsłego i „kokardki” zostawiam innym :)
Niestety szkoła wydaję się uczyć pojęć matematycznych w kolejności wg. odwrotności potencjalnej przydatności, ale dowodzi się tego wygodnie używając wektorów i łatwo wtedy zobaczyć dlaczego to prawda, jest to rozwiązane jako jedno z zadań tutaj:
http://ocw.mit.edu/courses/mathematics/18-02sc-multivariable-calculus-fall-2010/1.-vectors-and-matrices/part-a-vectors-determinants-and-planes/session-1-vectors/MIT1802SCpb1comb.pdf
@Jarosław Rzeszótko: Twierdzenie Talesa się spokojnie nada, a to wiedza szkolna. Wektory niby też, ale jakby wyższa szkoła ;)
Nie wiem czy rozwiązanie Torero jest prawidłowe, bo tak to zamotał, iż ciężko je zrozumieć. Podaję proste rozwiązanie:
Wystarczy zauważyć, że odcinek łączący dwa niezłączone wierzchołki czworokąta jest równoległy (to na podstawie twierdzenia Talesa), do obu nieprzecinających go, a interesujących nas odcinków (łączących te środki krawędzi). Mamy więc jedną parę równoległych boków, analogicznie postępujemy przy drugiej parze. Dwie pary równoległych boków dają równoległobok.
Co czytamy: „nie ogarniam, ale na wszelki wypadek przepiszę to samo jeszcze raz własnymi słowami, może nikt się nie zorientuje.”
A tak na prawdę: „ten Torero znowu nie umie jasno napisać i chyba on sam nie pewien, czy to dobre rozwiązanie (patrz ostatnie zdanie). Może specjalnie to tak zagmatwał? A w swoim gimnazjum to chyba nie miał nigdy geometrii”.
I tak mi zaimponowałeś, że byłeś w stanie podjąć się tego zadania, zważywszy twoje niektóre poprzednie wypowiedzi.
Raczej żaden nie ma szans na trafienie do Księgi (zwłaszcza z niedziałającego URLa) :)
http://en.wikipedia.org/wiki/ProofsfromTHE_BOOK
Hehe, przyganiał kocioł garnkowi:
http://en.wikipedia.org/wiki/ProofsfromTHE_BOOK
A nie, to jogger zamienia from na pochylone… http://u.42.pl/2JZQ
F@$# po prostu wyguglajcie „Proofs from the Book”
Bawiąc się apletem wymyśliłem banalny dowód… indukcyjny.
Czworokąt ABCD, środki boków EFGH. E leży na AB itd.
Warunek początkowy: jakikolwiek, na przykład kwadrat (środki boków też dają kwadrat, mamy równoległobok).
Krok: Przesunięcie któregokolwiek z wierzchołków (dla ustalenia uwagi A) o X i Y powoduje przesunięcie wierzchołków znajdujących się na bokach AB i AD (E i H) o X/2 i Y/2. |EH| bez zmian, czyli nadal |EH|=|FG|. |EF| i |GH| zmieniły się o tyle samo, czyli nadal |EF|=|GH|. Mamy równoległobok.
Przesuwając po kolei wierzchołki, możemy osiągnąć dowolny czworokąt.